Linear Discriminant Analysis

A linear Dimensionality Reduction technique for classification

It’s like PCA but focusses on separability among known categories ($t_i$)

Data

• Data is a set of $N$ input-output pairs
• Inputs are real-valued $d$-dimensional vectors ${\mathbf{x}}_i$
• Outputs $t_i$ indicate class membership of ${\mathbf{x}}_i$ , and are positive integers from 1 to $k$ (the amount of classes)
• Inputs are collected into $d\times N$ matrix $X$ and outputs into $N$-dimensional vector $\mathbf{t}$

Binary (Two Class) Classification Example

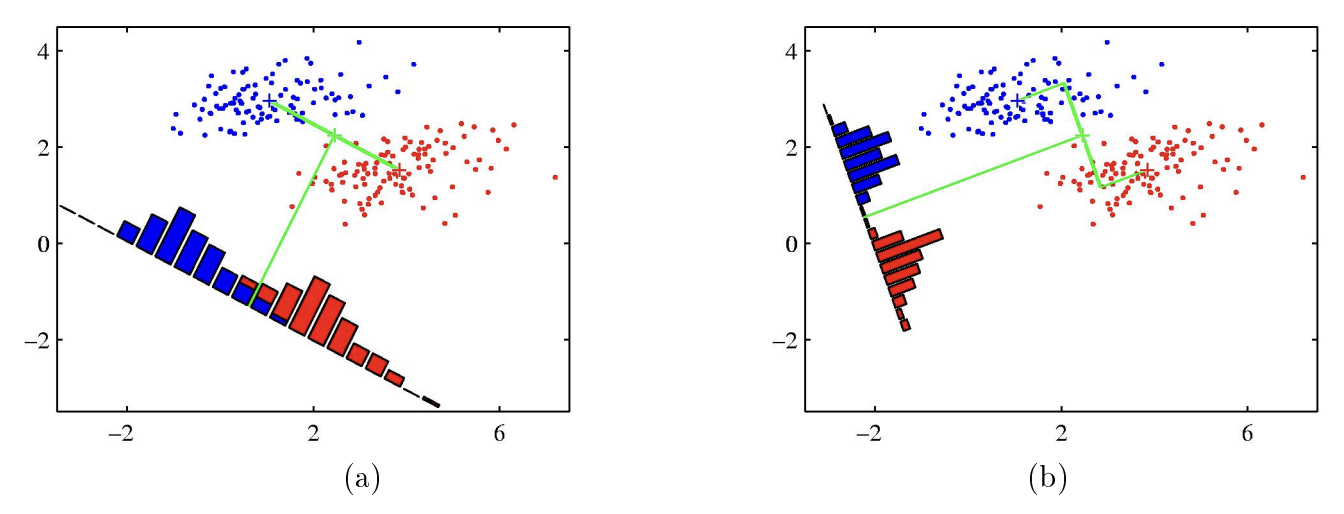
While a has greater variance, b has better separation between classes as there is less overlap between classes, making it ideal for classification problems.

Projection

LDA attempts to maximise the distance between the class means, while minimising variation (referred to as scatter in LDA) within each category.

Given a $d$-dimensional observation ${\mathbf{x}}_n$, we can project it down to a single dimension as before with:

$$y_n={\mathbf{w}}^T{\mathbf{x}}_n$$

Therefore, our aim is to find $\mathbf{w}$ as to maximise between class separation in the projected 1-d space. However, we need to decide how to quantify this, as we will in the following sections.

Means

Have $\bar{\mathbf{x}}$ be the mean of the input data as before in PCA

We define the class mean as

$${\mathbf{m}}_j=\frac{1}{N_j}\sum _{\left\{i:t_i=j\right\}}{\mathbf{x}}_i$$

With:

• $i:t_i=j$ meaning sample indexes $i$ belonging to class $j$
• $N_j$ being the total samples in class $j$

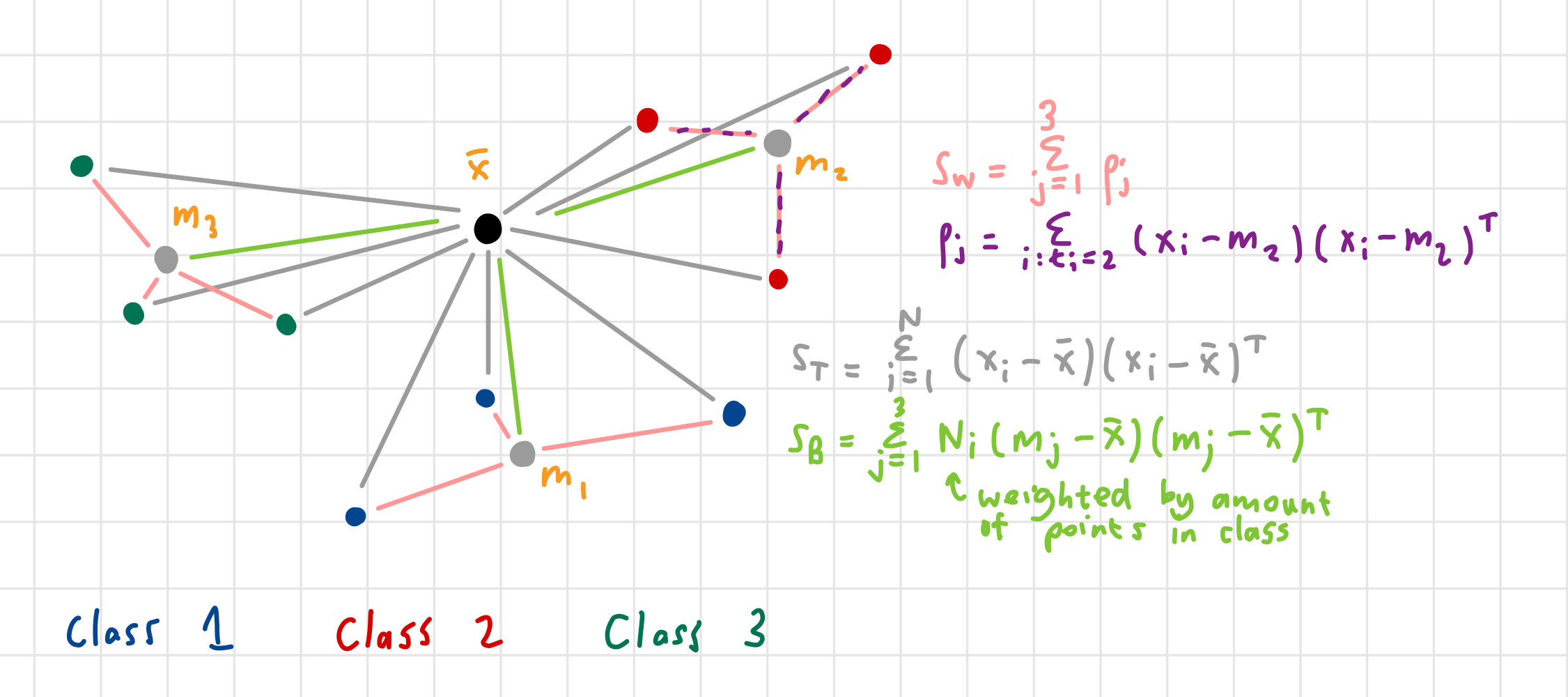
Scatter

• $S_T={\sum }_{i=1}^N({\mathbf{x}}_i-\bar{\mathbf{x}})({\mathbf{x}}_i-\bar{\mathbf{x}}{)}^T$ is the total scatter about the mean
• ${\rho }_j={\sum }_{\left\{i:t_i=j\right\}}({\mathbf{x}}_i-{\mathbf{m}}_j)({\mathbf{x}}_i-{\mathbf{m}}_j{)}^T$ is the within class $j$ scatter
• $S_W={\sum }_{j=1}^k{\rho }_j$ is the within-class scatter for the data
• $S_B={\sum }_{i=1}^N({\mathbf{m}}_{t_i}-\bar{\mathbf{x}})({\mathbf{m}}_{t_i}-\bar{\mathbf{x}}{)}^T={\sum }_{j=1}^k{N}_j({\mathbf{m}}_j-\bar{\mathbf{x}})({\mathbf{m}}_j-\bar{\mathbf{x}}{)}^T$ (where ${\mathbf{m}}_{t_i}$ is the class mean of the class to which sample $i$ belongs) is the between-class scatter.

Notice that $S_T=S_W+S_B$

Note: that scatter matrixes are unnormalised covariance matrices

Specifying the LDA axes

We want to find $v$ suitable axes collected into a $d\times v$ matrix $W$ so that we can transform our $d$-dimensional input $\mathbf{x}$:

$$\mathbf{y}=W^T\mathbf{x}$$

The scatters of data transformed this way, can be calculated:

$$W^T\bar{\mathbf{x}}$$

is the new data mean

$$\sum _{i=1}^N(W^T{\mathbf{x}}_i-W^T\bar{\mathbf{x}})(W^T{\mathbf{x}}_i-W^T\bar{\mathbf{x}}{)}^T=\sum _{i=1}^N{W}^T({\mathbf{x}}_i-\bar{\mathbf{x}})({\mathbf{x}}_i-\bar{\mathbf{x}}{)}^{T}W=W^T{S}_{T}W$$

is the new total scatter.

Likewise, we can show that the new between class scatter is $W^T{S}_{B}W$ and the within class scatter is $W^T{S}_{W}W$.

LDA aims to have points within the same class tightly clustered, while having clusters clearly separated

One objective for finding $W$ is to optimise

$$\underset{W}{\max }\frac{W^T{S}_{B}W}{W^T{S}_{W}W}$$

However, this is not clearly defined as the quotient of matrices does not exist. The maximisation of between class scatter (separation of clusters) and minimisation of within class scatter (tightly clustered classes) are in conflict and a tradeoff is to be made

As with PCA, we find the first axis vector $\mathbf{w}$

$$\underset{\mathbf{w}}{\max }\frac{{\mathbf{w}}^T{S}_B\mathbf{w}}{{\mathbf{w}}^T{S}_W\mathbf{w}}$$

Notice, as $\mathbf{w}$ increases without bound, the function will also grow boundlessly, therefore we add the constraint that it is unit vector:

$${\mathbf{w}}^T\mathbf{w}=1$$

This yields the constrained optimisation problem

$$\underset{\mathbf{w}}{\max }{\mathbf{w}}^T{S}_B\mathbf{w}\text{ subject to }{\mathbf{w}}^T{S}_W\mathbf{w}=1$$

Hey! Its a Lagrange Multipliers problem! Let’s solve it:

$$\begin{array}{c}f(\mathbf{w})={\mathbf{w}}^T{S}_B\mathbf{w}\\ g(\mathbf{w})=1-{\mathbf{w}}^T{S}_W\mathbf{w}\end{array}$$

The Lagrangian is:

$$\mathcal{L}(\mathbf{w},\lambda )={\mathbf{w}}^T{S}_B\mathbf{w}+\lambda \cdot (1-{\mathbf{w}}^T{S}_W\mathbf{w})$$

Which can be solved

$$\begin{array}{c}{\nabla }_{\mathbf{w}}\mathcal{L}=2S_B\mathbf{w}-2\lambda S_W\mathbf{w}=0\\ S_B\mathbf{w}=\lambda S_W\mathbf{w}\end{array}$$

This is not quite a eigenvalue problem since $S_W$ is in the way, but if we assume $S_W$ is invertible:

$$S_W^{-1}{S}_B\mathbf{w}=\lambda \mathbf{w}$$

it becomes an eigenvalue problem for $S_W^{-1}{S}_B$ , with solutions for $\mathbf{w}$ being the eigenvectors corresponding to the largest eigenvalues!

How about if $S_W$ is not invertible?!

$S_W$ is not invertible if it isn’t full rank (has some zero eigenvalues).

We can find a solution in two steps:

1. use PCA on $S_W$ to remove empty dimensions, making the transformed data invertible
2. Scale the axes so that orthogonal transformations do not change within class scatter (i.e. whiten the class centered data)
   • Whitening: $(Q_r{\Lambda }_r^{-1/2}{)}^T{S}_W(Q_r{\Lambda }_r^{-1/2})=I$

After whitening we have a new objective ${\mathbf{w}}_{\ast }$

TODO: Finish this up!