Lagrange Multipliers

Finding local minima or maxima given a constraint. We find the minimum and maximum points of the function f(x, y) given g(x, y) = 0 (constant).

Let’s explain this by way of an example:

Given the function $f(x,y)=xy+1$ , we observe it has no absolute minimum or maximum

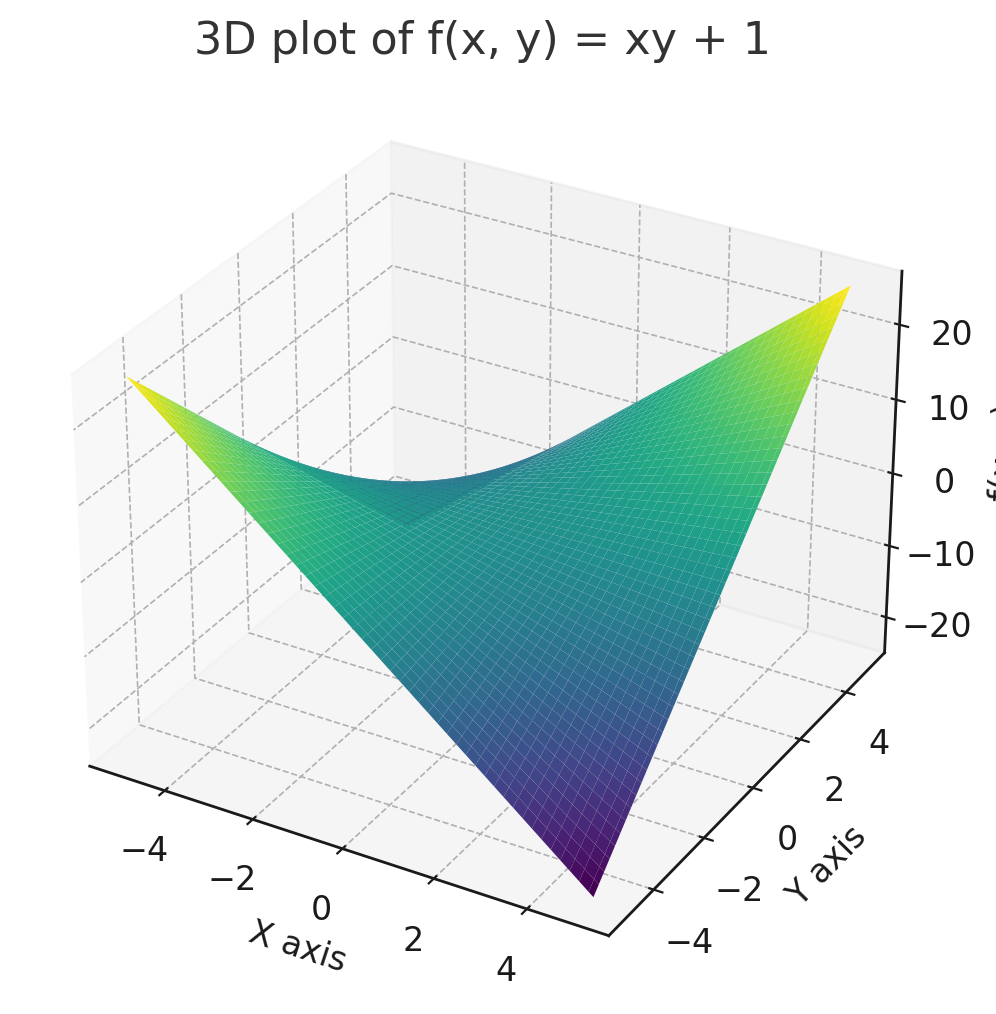
However, by introducing a constraint, such as $g(x,y)=0=x^2+y^2-1$ (a circle), we may find the local minima and maxima on the curve (in red)

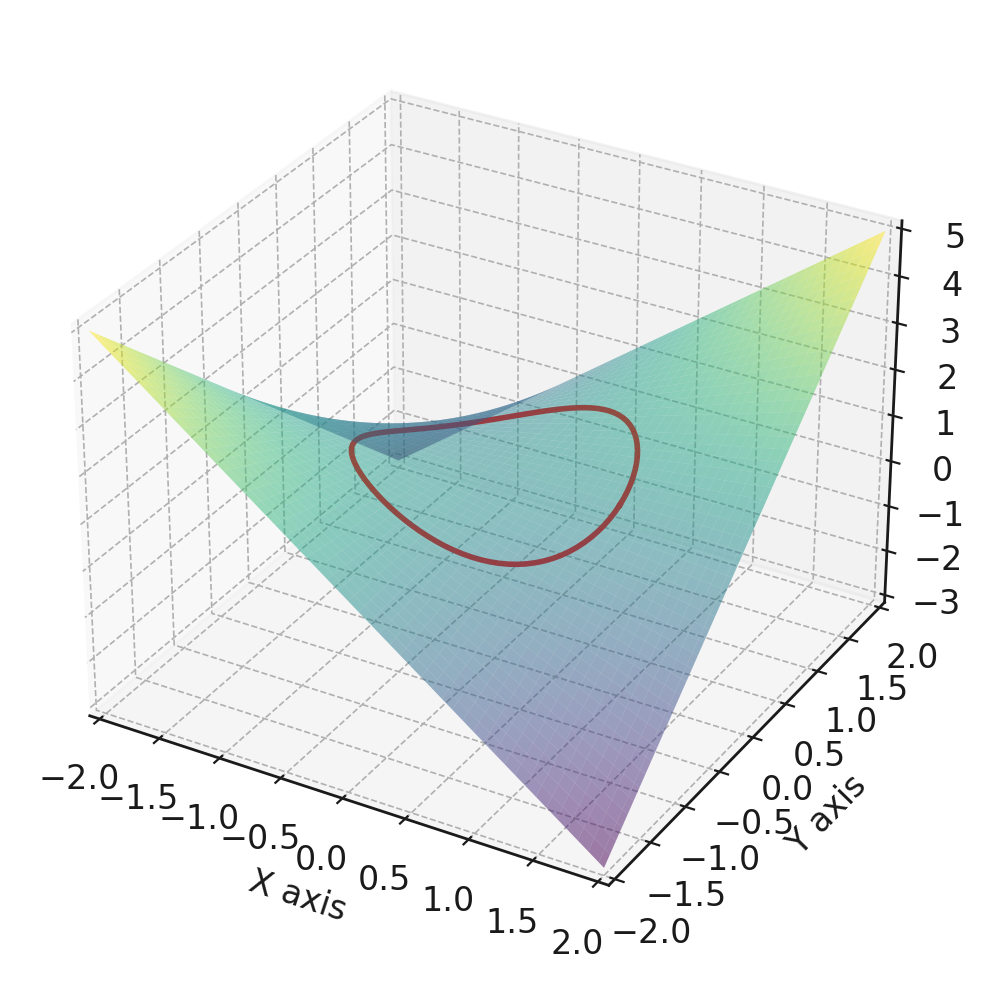
Observing the level curves, we’re interested in the contours that barely touch the constraint curve. These are the local minima and maxima we’re interested in.

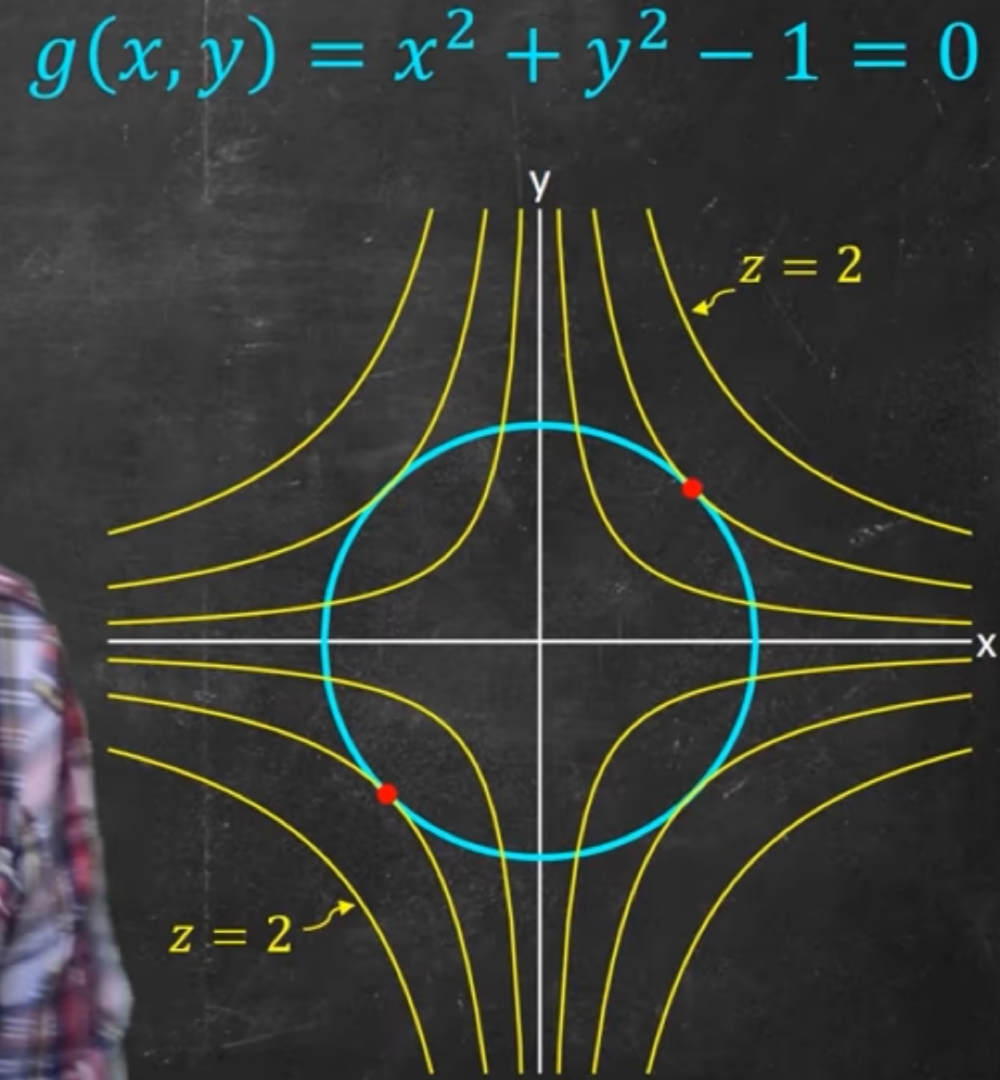
This means the local minima and maxima are points at which both the constraint curve and level curve have the same tangent line, but also normals in the same direction

The gradient vector is normal to the level curves such that $\nabla g$ and $\nabla f$ are scalar multiples. We introduce the Lagrange Multiplier $\lambda$ to represent this relationship

$$\nabla f=\lambda \nabla g$$

We can solve the two equations simultaneously:

$$\begin{array}{c}\nabla f=\lambda \nabla g\\ g(x,y)=0\text{ as was given}\end{array}$$

Alternatively, we can introduce a auxiliary function, called the Lagrangian to combine these conditions:

$$\mathcal{L}(x,y,\lambda )=f(x,y)+\lambda \cdot g(x,y)$$

and solve for

$${\nabla }_{x,y,\lambda }\mathcal{L}(x,y,\lambda )=0$$

For the example we’ve been concerned with

$$\begin{array}{c}\mathcal{L}(x,y,\lambda )=xy+1+\lambda \cdot (x^2+y^2-1)\\ {\nabla }_{x,y,\lambda }=0=\left[\begin{array}{c}y+2\lambda x\\ x+2\lambda y\\ x^2+y^2-1\end{array}\right]\end{array}$$

This yields three equations for 3 unknowns, which when solved simultaneously will give the four local minimums and maximums:

$$x=\pm \frac{1}{\sqrt{2}}\text{ and }y=\pm \frac{1}{\sqrt{2}}$$