Dimensionality Reduction

Introduction

• Models we fit typically have high dimensional inputs
• These models consider not just the inputs separately, but also the interactions between inputs.
• This requires each input to have parameters in the model, resulting in a model that scales, often super-linearly, with the input dimension.

Dimensionality reduction allows us to reduce the number of dimensions, and thereby the number of parameters

This is made possible by the following assumptions:

• Data can be approximated in a lower-dimension
• Data occupies a lower-dimensional manifold (lie on some form of lower dimensional curve)
  • The transformations in this course will transform the input vectors by projecting them onto a lower-dimensional euclidean (flat planes) subspace.

Input and Feature Space

Before we look at the techniques, we have to understand some basic linear algebra:

• Given two $d$-dimensional vectors $x$ (input) and $a$ (unit vector)
• $a\cdot x=a^{T}x$ will be the length of the projection of $x$ onto $a$, this length is known as the score of $x$ for feature $a$
• If we have multiple unit vectors, we can collect them into a matrix $A$ with one column per feature, $A^{T}x$ computes a vector of scores.
• This vector is known as the feature vector of $x$ for the feature space defined by $A$
• Assuming $A$ is $d\times k$, with $k\le d$, since $x$ is a $d\times 1$ vector, $A^T$ is $k\times d$ making the resulting feature vector $k\times 1$, hence reducing the dimension to $k$

This is the foundation for dimensionality reduction, we need to find a subspace A from our input space that represents the data ‘well’

We’d like the techniques not to be dependant on the axis system, thus we choose features that remove dependance on the input axes. These changes in axes system could be:

• Permutation (order of attributes changed)
  • PCA orders axes based on importance (max variation)
• Translating the origin (Celsius to Kelvin)
  • Subtract mean to remove effects of translation (note subtraction does not affect the relative position of the data points)
• Scaling the axes
• Reflecting the axes
• Rotating the axes

Projection is robust against these, except for translation, hence the subtraction of the mean

Techniques

Two techniques are discussed, each with the goal of projection onto a lower-dimensional subspace while retaining data characteristics of interest:

• Principle Component Analysis
  • Unsupervised
• Linear Discriminant Analysis
  • Supervised

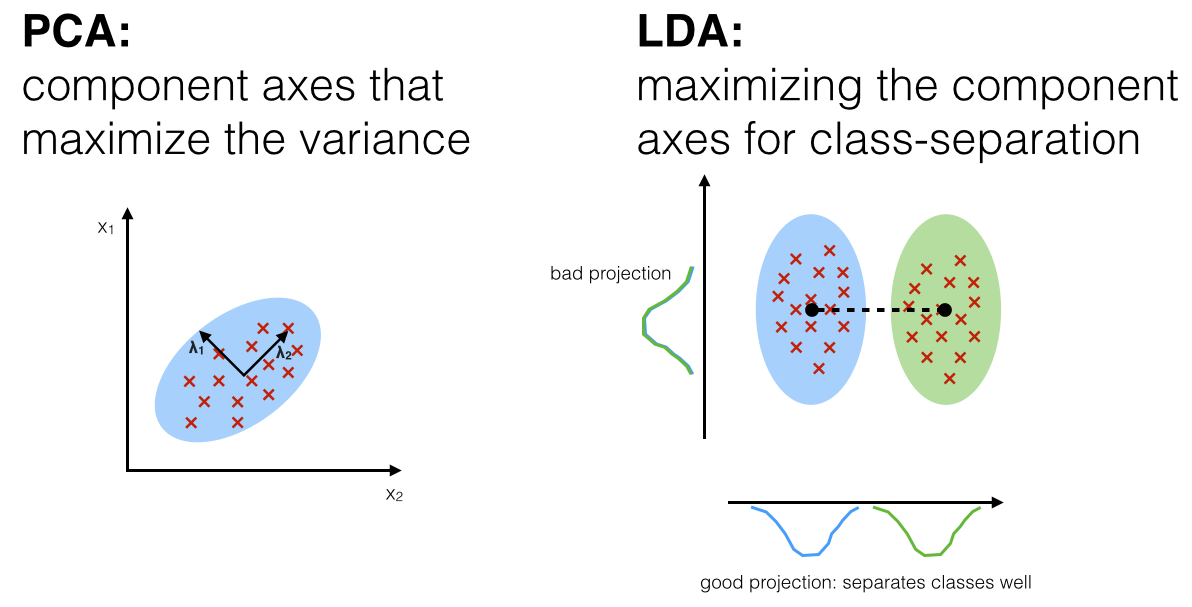
PCA finds component axes that maximises the variance while LDA axes maximises class-separation (between class scatter)